The dictatorship of consortia
on the media they own

Let's dive into the data

The data we get from the Quotebank-dataset look like this :

data.head()

For now, our only way to identify in which newspaper a quote was published is the url where the quote was discovered. To be able to characterize clusters of newspapers, we need to extend our datasetwith the newspaper's entity, as well as the media group owning it. Because we expect to see media differences based on their country of origin, we also add the home country of the media. Using our best scraping skills we query Wikidata to add those features. This comes at a cost, because not all newspapers have a Wikidata entry and of those, not all have a media group indicated. As a consequence, the reduced dataset contains around 1'000 newspapers which reduces the diversity of our data in exchange for more insight on each data point. Single journals in a group were also removed because they would be irrelevant to our goal to cluster them according to their parent group.

newspaper_info.head()

Now that we have the data we process it

Since for each sample, we have both quotes, and quotees (i.e. the people quoted), it seems natural to try and cluster journals according to these two features, and some measure of their similarity. Let us then try two different methods:

• First, we will cluster newspapers according to which speakers are cited in it.
• Secondly, we will cluster newspapers according to the text content  of their quotes.

For both of these features, we created the associated TF-IDF matrix, namely a matrix [newspaper x speaker] and another [newspaper x token]. In a nutshell, this method allows one to measure the importance of a term (here a citee, or a word) to a document (here a media) in a collection (here, all the media we have kept) based on its number of apparitions. To do so, this method gives to each word in a document a weight proportional to its number of occurrences in document (TF: Term Frequency) and inversely proportional to its 'presence' in the corpus (IDF: Inverse Document Frequency). To quantify the 'presence' of a word in the corpus, we simply count the number of documents in which it occurs –we don't take its occurrences per document into account here.

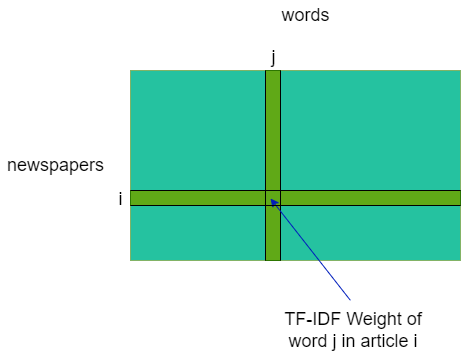
These matrices give us a representation of the newspaper in the words and speakers spaces. The problem is that the data (our TF-IDF matrices) is inherently high-dimensional (speaker: ~210'000 dimensions, words: ~260'000 dimensions), so we as humans can not directly visualize it, even computers struggle to run cluster algorithm in these dimensions.

How can we analyze data which lies in such a high dimension?

In order to tackle this challenge, we will project the newspapers in a lower dimension space using Singular Value Decomposition (SVD).
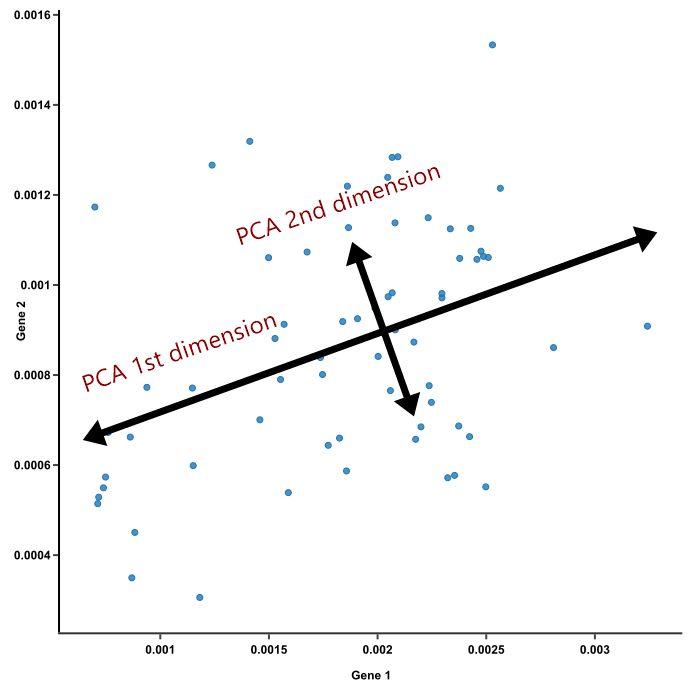
This transformation should allow us to extract topics, which correspond to the directions of highest variation, i.e. the ones separating the media the best, and their importance. We can then view the differences between different media along one such axis. Refer to our notebook for more technical details.

Let us apply this technique on the speakers matrix first

Each of the following plots represent a projection of the media (as represented in the speakers TF-IDF matrix) along some of the axes mentioned above. The x-axis corresponds to the first axis mentioned in the legend, and the y-axis to the second.
Each point corresponds to a media, and its color indicates the group owning it.

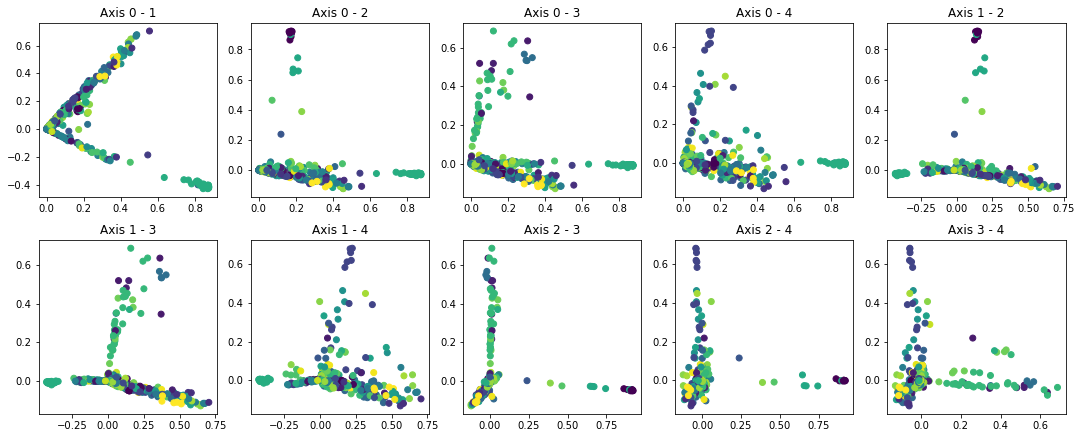
By applying SVD on the speaker TF-IDF matrix and looking into the speakers contributing the most to each axis, we identify the following trends for each axis:

The axes are sorted by how well they separate the newspapers. As we can see, the best criterion to separate newspapers in two categories is to split them into the ones treating local information (eg: a local journal at Canberra) and the ones treating worldwide information such as the New York Times. From the subsequent axes, we can see that the country of origin of a newspaper is the main criterion in speaker based clustering. This makes sense: UK-media will cite more UK-speakers, while US-media will cite more US-speakers. A good example of that is the Newsquest Media Group, UK's second largest publisher of regional and local newspapers. This group's newspapers are located at the far right of the first plots (dark green dots), and are well clustered far from the others. We can see that media are diverse with respect to their countries of origin. However, even if one is aware they should get their information from different media, are they really that likely to get it from different countries' media? Now let us see if we can differentiate the media inside one country! We will focus on the USA since it is the country with the most data available

Again we extract the trends from the list of top speakers per axes:

We also see (in bright green above) that journals from Townsquare Media explain most of the variance of several axes, namely the 3rd and the 4th and are very well clustered from the rest. Hence although we can visually recognize media from this group, it might be interesting to reproduce our analysis while removing Townsquare Media's newspapers. These are the resulting projections:

Clearly we can spot some clusters when projecting on the first few axes. The purple and yellow ones are especially well separated and respectively correspond to a media specialized in local news of North of the US and a US radio media conglomerate.

What we learnt

We have seen that at a worlwide scale as well as at the local US scale, looking at the speakers to differentiate newspaper groups leads to a clustering mostly geographical as opposed to thematic. This is due to local newspapers mentioning local celebrities. We will now look at the same study but from the quoted text perspective and try to see if we can obtain a 'better' clustering of media groups.

What about the quotes?

Now let us apply this technique on the words' matrix (constructed with the words from the quotes). For starters we will consider all the quotes, and not only the ones in US newspapers. We expect there is still some geographical distinction –due for example to cultural differences, or diverging points of interest (e.g. American football is popular in the USA, but not much in other English speaking countries)– However, we do not expect them to be as obvious as with the speakers' matrix, since we expect more topics convergence between newspapers of different countries.

Again, using the top words per axis we can identify the trends corresponding to the axes:

Our hypothesis is verified, as we have found topics of divergence between newspapers not related to its geographical origin. However, clustering in these cases produces poor result for identifying media consortiums with the notable exception of the bright green points that can be seen at the top of axes 0-4 projection.

To try and obtain better clustering, we will now only focus on the USA again:

As always, we try and identify the trends corresponding to the first axes:

As you can see, they are similar to the previous ones –with unsurprisingly no "country separation axis" anymore. Visually, the bright green points really stand out, can you guess to which journal they correspond?
Of course it is Townsquare media once again, which stands out. That's interesting: it is not only divergent with respect to its choice of speaker, but also w.r.t. the subjects it treats. We hypothesize it is so particular because it is composed of many *local radio stations*. Once more we will remove this consortium from our analysis, and see what results we get:

The trends we identify are as follow:

We can note that axes 0, 1 and 2 are identical to the previous ones. Axis 3 is quite similar also, but if you delve into the details of the words identifying it, you can see they are less related to specific states (e.g. words "Wyoming" or "Montana"), but rather to states in general. The projections are now clearer (especially along axes 1-4 (yellow/purple)), and that for 2 reasons mainly:

1. The withdrawal of articles from Townsquare media, which had a high variance among several axes. It removed their influence, and hence the SVD projection could take into account the other media more.
2. The removal of some points makes it easier to see the rest of them.

In general, projections originating from the speakers-matrix give better visually separated results, yet they are less meaningful (in the sense that the separation is mostly geographical) than the ones originating from the words-matrix.
Indeed, one can see that graphs from the latter are more entangled.
Therefore, although both matrices allow for some clustering of the owner groups, we deem the 2nd one to be more useful.

Note that if you are still thirsting for more exploration, and you don't want to rerun our code with your own parameter, we have prepared for you some interactive bokeh-plots. One can access them by clicking the links on the upper-left of our website.